以太坊源码解读(7)以太坊P2P网络
一、分布式网络的来历
基于P2P技术的应用有很多,包括文件分享,即时通信,协同处理,流媒体通信等等。其中文件分享和下载是p2p技术最集中体现。其中,DHT技术是目前很多分布式系统所普遍采用的方案,也包括以太坊。所以这里先要对DHT技术有所了解。
二、DHT(Distributed Hash Table)技术简介
DHT全称叫分布式哈希表(Distributed Hash Table),是一种分布式存储方法,一类可由键值来唯一标示的信息按照某种约定/协议被分散地存储在多个节点上,这样可以有效地避免“中央集权式”的服务器(比如:tracker)的单一故障而带来的整个网络瘫痪。
1)首先我们需要弄懂一个概念——哈希表。
哈希表是一种数据结构,是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做哈希表。
 (数组与链表的结合)
(数组与链表的结合)
哈希表的具体实现过程是:把Key通过一个固定的算法函数既所谓的哈希函数转换成一个整型数字,然后就将该数字对数组长度进行取余,取余结果就当作数组的下标,将value存储在以该数字为下标的数组空间里。这个数组空间,我们可以称之为一个“bucket”,也就是说bucket里存的是多个键值对,键值对以链表的形式组织。
某个具体的哈希表,bucket的数量通常是固定的(比如N个),桶的编号从0~N-1,分别就是上面取余之后的结果。当使用哈希表进行查询的时候,就是再次使用哈希函数将key转换为对应的数组下标,并定位到该空间获取value,如此一来,就可以充分利用到数组的定位性能进行数据定位。
特点:这种哈希表的特点是创建哈希表(HashMap)需要先指定大小,这导致如果哈希表存满了要扩容的时候就会有很大麻烦。
举个例子:
假设哈希函数为 hash(x)=x ,哈希表的长度为5(有5个桶)
key=6时,hash(6)%5 = 1,即Key为6的元素存储在第一个桶中
key=9时,hash(9)%5 = 4,即Key为9的元素存储在第四个桶中
Key=17时,hash(17)%5=2,即Key为17的元素存储在第二个桶中....假设现在hash表长度扩容成8,那么Key为6,7,8 的数据全都需要重新哈希。因为,
key=6时,hash(6)%8 = 6,即Key为6的元素存储在第六个桶中
key=9时,hash(9)%8 = 1,即Key为9的元素存储在第一个桶中
Key=14时,hash(14)%8=6,即key为14的元素存储在第六个桶中....
从上可以看出:扩容之后,元素的位置全变了。所以哈希表在创建后就不要轻易的扩容。
2)什么是分布式哈希表?
DHT全称叫分布式哈希表(Distributed Hash Table),是一种分布式存储方法。在不需要服务器的情况下,每个客户端负责一个小范围的路由,并负责存储一小部分数据,从而实现整个DHT网络的寻址和存储。DHT技术的应用来源于p2p网络发展的需要。第二代p2p文件共享系统正是由于查找节点十分困难且耗费网络资源而促进了第三代系统引入了DHT技术,用以快速的查找节点以及资源。
2.1 异同 分布式哈希表与哈希表的共同之处在于能够实现快速的查找。它与上面哈希表的不同在于:1)哈希表通常是本地的,用于在本地快速的插入和查找数据。而分布式哈希表相当于将哈希表中的bucket分散到不同的节点计算机中。2)哈希表增添、删除桶会导致所有的数据需要重新hash,但分布式哈希表支持动态的节点的数目,节点可以随意的进入或退出。
2.2 一致性哈希 这种动态节点是如何实现的呢?不得不提的就是一致性哈希。一致性哈希的具体实现我们这里不作介绍,我们只要知道它是一种经典的分布式哈希表的实现方法。它是对机器(通常是其IP地址)和数据(通常是其KEY值)进行统一的运算,把他们全都映射到一个地址空间中。假设我们需要把值映射到32bit的地址空间,那么我们的地址就可以分布在从0到2^32 – 1的范围内。然后我们将这些地址首尾相连构成一个环状,即一致性哈希的拓扑结构。

如上图,A、B、C、D、E五个节点分别在整个地址空间的5个位置,分别负责由其上一个节点到本节点的地址空间,即A负责E~A的地址空间上的所有数据,B负责A~B的地址空间的所有数据,以此类推。如果某一数据(KEY值)映射到地址空间上的位置在AB之间,那么这部分数据将储存在B节点上。
因此,当有一个新的节点插入的时候,比如AB之间插入一个A',那么整个网络上其他节点的储存是不用变的,只要移动一部分B节点上的数据到A'上即可。
2.3 路由表:实现快速查找
使用分布式哈希表快速的查找指定的数据在哪个节点,即数据定位,是通过特殊的路由方案解决的。最普通的路由方案就是当一个节点接收到某个“key”的查询时,先看 key 是否在自己这里。如果在自己这里,就直接返回信息;否则就把 key 转发给自己的继任者。以此类推。
这种玩法的时间复杂度是 O(N)。对于一个节点数很多的 DHT 网络,这种做法显然非常低效。
成熟的DHT技术中使用的是更加高级的路由方案,比如在Chord中,用到一个叫做“Finger Table”的机制,或者在Kademlia中所使用的"K-桶",其实就是一种特殊的路由表。而路由表的目标就是:尽可能地将查询key发送到离存储这个key最近的那台机器上。
上面提到的Chord和Kademlia是两种不同的DHT技术,他们所实现的DHT具有不同的拓扑结构,自然也就有不同的查询方案(路由表)。Chord所采用的拓扑结构就是上面所说的环形结构,我们来简单看看Chord的拓扑结构中如何进行路由以及如何插入新节点。
【“Finger Table”】
指针表(Finger Table)是每个节点都持有的一个路由表,这个表最多包含m项(m是散列值的比特数),从0~m-1算起,每一项都对应着某一个节点的ID,其中第i项与其对应的节点ID的关系是:(n+2^) mod 2^m。

【查询】当某个节点收到某个key的查询时,先在本地查找,如果没有则选择最大的且不超过key的那一项,然后把 key 转发给这一项对应的节点,递归执行上面查找过程,知道找到对应的数据。
【节点插入】节点接入网络时,首先与任意一个已知节点建立连接,通过指针表查询到自己节点ID的“前任”节点和“继任”节点。然后将该节点插入到拓扑结构中,并与其相邻的节点调整并获取节点内容。
【节点正常退出】
如果某个节点想要主动离开这个 DHT 网络,按照约定需要作一些善后的处理工作,比如通知前任节点去更新其继任节点。
【节点异常异常】
作为一个分布式系统,任何节点都有可能意外下线。为了保险起见,Chord 引入了一个“继任者候选列表”的概念。每个节点都用这个列表来包含:距离自己最近的 N 个节点的信息,顺序是【由近到远】。一旦自己的继任者下线了,就在列表中找到一个【距离最近且在线】的节点,作为新的继任者。然后 节点A 更新该列表,确保依然有 N 个候选。更新完“继任者候选列表”后,节点A 也会通知自己的前任,那么 A 的前任也就能更新自己的“继任者候选列表”。
Chord 就介绍到这里,我们的重点是Kademila,因为实际应用的 DHT 大部分都采用 Kad 及其变种,包括以太坊的分布式网络。想要进一步了解的话可以参考其原创论文:
《Chord——A scalable peer-to-peer lookup service for internet applications》
三、Kademlia协议
与Chord不同,Kademlia所用的拓扑结构是二叉树。
二叉树知识补充
在计算机科学中,二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。
特点:
1、树的深度:树中最大的结点层。深度为k的完全二叉树,至多有2k-1个叶子节点,至多有2k-1个节点。
2、树的结点(node):包含一个数据元素及若干指向子树的分支;
3、孩子结点(child node):结点的子树的根称为该结点的孩子;
4、双亲结点:B 结点是A 结点的孩子,则A结点是B 结点的双亲;
5、兄弟结点:同一双亲的孩子结点; 堂兄结点:同一层上结点;
6、结点的度:结点子树的个数;
7、叶子结点:也叫终端结点,是度为 0 的结点;
在Kad网络中,所有节点都被当作一颗二叉树的叶子,并且每一个节点的位置都由其ID值的最短前缀唯一确定。
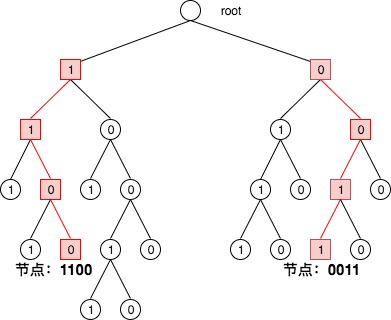
Q1:如何把节点映射到二叉树?
1)先把key以二进制的形式表示,进行“最短唯一前缀”来处理;
2)二进制的第n位代表二叉树的第n层,这样一个子树的每个节点连起来就是完整的id二进制表示;
3)“1”代表进入左子树,“0”代表进入右子树(反过来也行)
4)按上面的步骤处理后得到到最后的叶子节点,就是该“key”对应的节点。
Q2:Kad网络的路由机制是怎样的?
【二叉树的拆分】对于任意一个节点,都可以把这个二叉树分解为一系列连续的,不包含自己的子树。最高层的子树,由整棵树不包含自己的树的另一半组成。下一层子树由剩下部分不包含自己的一半组成,以此类推,知道分割完整棵树。
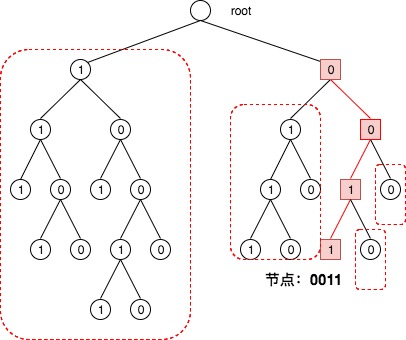
Kad 默认的散列值空间是 m=160(散列值有 160 比特),因此二叉树最大深度为160,拆分出来的子树最多有 160 个。如上图中,节点的最小前缀为0011,节点深度为4,刚好拆分出4个子树。
每个节点都能够以自己的视角拆分整个二叉树。对于每一个节点而言,当它以自己的视角完成子树拆分后,会得到 n 个子树;对于每个子树,如果能知道里面的一个节点,那么它就可以利用这 n 个节点进行递归路由,从而遍历整个子树的所有节点。
【K-桶】上面说的知道子树的一个节点就可以遍历整个子树,但实际上由于分布式系统的节点总在变化,所以Kad网络规定了每个节点要记录每个拆分子树中的K个节点(比如BT下载设定K=8)。这样每个子树的K个节点被记录在一个路由表中,节点如果有n个拆分子树就要控制n个路由表。这里的路由表就是所谓的“K-桶”。
针对上图的id=0011节点,应该有四个k-桶:
| i | 距离 | 节点信息 |
| 0 | [2^0, 2^1) | (ip, udp port, node ID)0-1 (ip, udp port, node ID)0-2 ... (ip, udp port, node ID)0-k |
| 1 | [2^1, 2^2) | (ip, udp port, node ID)1-1 (ip, udp port, node ID)1-2 ... (ip, udp port, node ID)1-k |
| 2 | [2^2, 2^3) | (ip, udp port, node ID)2-1 (ip, udp port, node ID)2-2 ... (ip, udp port, node ID)2-k |
| 3 | [2^3, 2^4) | (ip, udp port, node ID)3-1 (ip, udp port, node ID)3-2 ... (ip, udp port, node ID)3-k |
这里节点的【距离】是通过异或的二进制计算得来:

这两点的距离就是2^5 + 2^2 = 36。因此上面的四个k-桶就分别储存了距离从近到远的四个范围的k个节点。【可以把这种计算当成是二叉树上两个节点距离的计算方式】
需要注意的是,k-桶的列表不是一成不变的,而是不断刷新的。每个k-桶内部存放信息的位置是根据上一次看到的时间顺序排列的,最近(least-recently)看到的放在头部,最后(most-recently)看到的放在尾部。PING不通的节点要进行删除。
Q3、新节点添加的时候会有哪些动作?
新节点加入时,主要是先要构建自己的k-桶,需要进行如下步骤:
1)新节点首先向任意一个节点发起查询请求(FIND_NODE),查询自己的ID;
2)节点收到请求后,按照距离把新节点放到自己对应的K-桶中,然后按照协议找到K个与新节点最接近的节点返回;
3)新节点收到返回的节点信息后,即可初始化自己的k-桶,并向这些节点发送查询请求,如此往复(递归),建立起自己的路由表。
当旧节点收到一个新节点信息的时候,要进行如下步骤:
1)计算自己与新节点的距离,根据这个距离,选择对应的k-桶进行操作;
2)如果新节点的ip已经在这个k-桶,则将这一项移动到k-桶的尾部;
3)如果新节点的ip不在这个k-桶:
a)如果k-桶记录小于k,则直接把发送者添加进去;
b)如果k-桶记录大于等于k,则选择头部的节点进行PING操作,如果没有响应,则删除这个节点,添加新节点到尾部;如果有响应,就忽略新节点;
Kad 就介绍到这里。如果想了解更多,可以参考其论文:
《Kademlia——A Peer-to-peer information system based on the XOR Metric》
p2p网络的基本知识我们先介绍到这里,下一节开始介绍以太坊基于kad网络的p2p源码解析。
回顾一下,前面说到以太坊分布式网络采用了Kademlia协议,它的特点是: 1、采用了二叉树的拓扑结构; 2、每个节点都对整树进行拆分,分成n棵子树; 3、从每棵树中取K个节点, ...