算法:分而治之
在分而治之的方法中,手头的问题被分成较小的子问题,然后每个问题都独立解决。当我们继续将子问题划分为更小的子问题时,我们最终可能会达到无法进行更多划分的阶段。解决那些“原子”最小可能的子问题(分数)。最后合并所有子问题的解决方案以获得原始问题的解决方案。
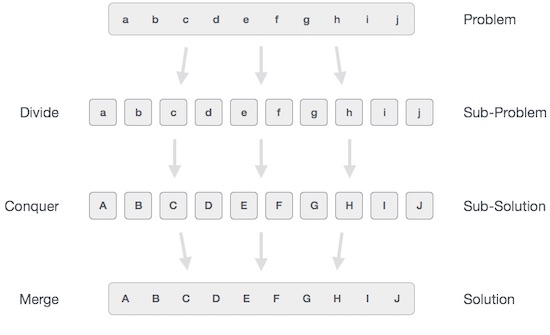
从广义上讲,我们可以通过三个步骤来理解 分而治之的 方法。
分割/歇
此步骤涉及将问题分解为更小的子问题。子问题应该代表原始问题的一部分。此步骤通常采用递归方法来划分问题,直到子问题不再可被整除为止。在这个阶段,子问题本质上是原子的,但仍然代表了实际问题的某些部分。
征服/解决
这一步收到了许多较小的子问题需要解决。通常,在这个层面上,问题被认为是自己“解决”的。
合并/合并
当解决较小的子问题时,该阶段递归地组合它们直到它们形成原始问题的解决方案。这种算法方法递归地工作并且征服和合并步骤的工作如此接近以至于它们看起来像一个。
例子
以下计算机算法基于 分而治之的 编程方法 -
- 合并排序
- 快速排序
- 二进制搜索
- Strassen的矩阵乘法
- 最近的一对(点)
有多种方法可以解决任何计算机问题,但所提到的是分而治之的方法的一个很好的例子。
动态编程方法类似于将问题分解为更小但更小的子问题的分而治之。但不同的是,分而治之,这些子问题并没有独立解决。相反,记住这些较小子问题的结果并用于类似或重叠的子问题。动态编程用于我们遇到问题的地方,可以将其划分为类似的子问题, ...