编程宝库 - 技术改变世界

编程宝库

Search

C语言编程技术

C++实现去除字符串头尾指定字符

QT实现简单计算器功能

C语言解析二叉树

二叉树分类

满二叉树

除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。也可以理解为每一层的结点数都达到最大值的二叉树。

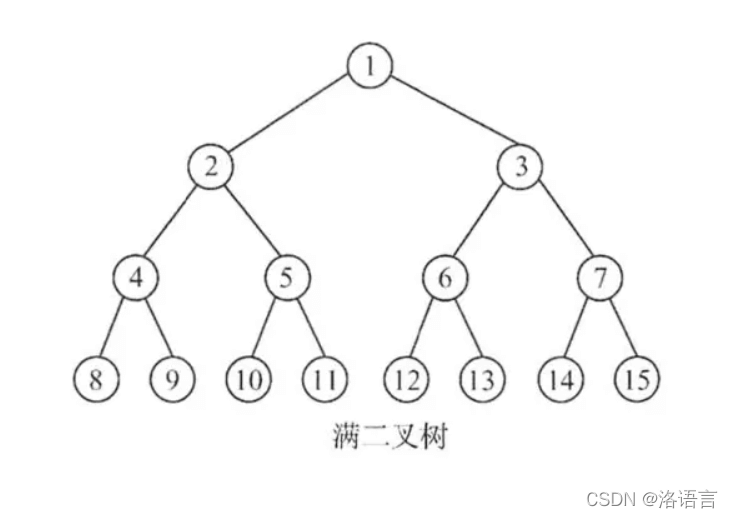
完全二叉树

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

简单的说，完全二叉树就是最后一层可以有缺失的满二叉树(完全二叉树是一种特殊的满二叉树)，并且是从右往左的缺失。

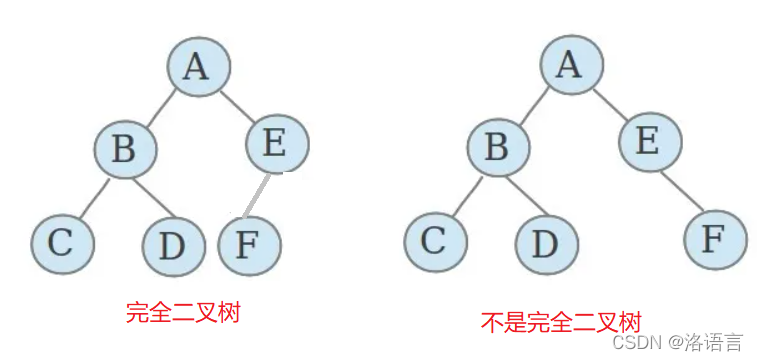
二叉树性质

若规定根节点的层数为1，则一棵树非空二叉树的第 i 层上最多有2^(i-1)个节点。
若规定根节点层数为1，则深度为h的二叉树的最大节点数是2^h−1
对任何一颗二叉树，如果叶节点(度为0的节点)个数为 n0 ，度为 2 的节点个数为 n2 ，则n0 = n2 + 1。
若规定根节点层数为1，具有N个节点的满二叉树的深度为小于（log_2）N+1的最大整数。

性质的使用

在具有 2n 个结点的完全二叉树中，叶子结点个数为( )

A n

B n + 1

C n - 1

D n / 2

分析：

设度为 0 的结点有 x0 个

设度为 1 的结点有 x1 个

设度为 2 的结点有 x2 个

x0 + x1 + x2 = 2n

x0 = x2 + 1

由上面两个式子可推出：2 * 2x2 + x1 + 1 = 2n

因为是完全二叉树，x1 可能是0，1，但是要使上式结果为偶数，x1只能是1，所以 x2 等于n ，选A。

二叉树的遍历

首先我们先创建一个简单的二叉树

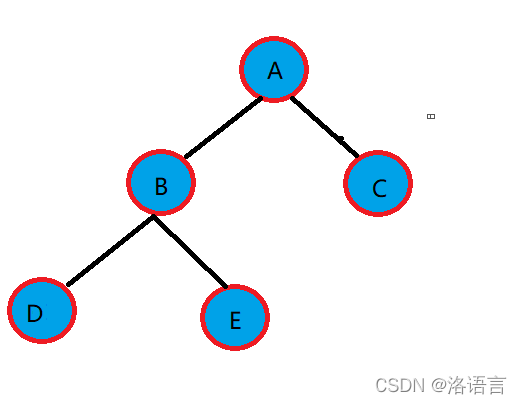
typedef char BTDataType;
typedef struct BinaryTreeNode {
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;
int main()
{
	BTNode* A = (BTNode*)malloc(sizeof(BTNode));
	A->data = 'A';
	A->left = NULL;
	A->right = NULL;
	BTNode* B = (BTNode*)malloc(sizeof(BTNode));
	B->data = 'B';
	B->left = NULL;
	B->right = NULL;
	BTNode* C = (BTNode*)malloc(sizeof(BTNode));
	C->data = 'C';
	C->left = NULL;
	C->right = NULL;
	BTNode* D = (BTNode*)malloc(sizeof(BTNode));
	D->data = 'D';
	D->left = NULL;
	D->right = NULL;
	BTNode* E = (BTNode*)malloc(sizeof(BTNode));
	E->data = 'E';
	E->left = NULL;
	E->right = NULL;
	A->left = B;
	A->right = C;
	B->left = D;
	B->right = E;
	LevelOrder(A);
}

前序遍历

前序(先序)：根 -> 左子树 -> 右子树

预期结果：A B D E C

//前序
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		//为了结果更加直观，将NULL打印
		printf("NULL ");
		return;
	}
	//先打印根的数据
	printf("%c ", root->data);
	//遍历左子树
	PrevOrder(root->left);
	//遍历右子树
	PrevOrder(root->right);
}

编译结果：

中序遍历

中序：左子树 -> 根 -> 右子树

预期结果：D B E A C

void MidOrder(BTNode* root)
{
	//为了结果更加直观，将NULL打印
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	MidOrder(root->left);
	printf("%c ", root->data);
	MidOrder(root->right);
}

编译结果：

后序遍历

后续：左子树 -> 右子树 -> 根

预期结果：D E B C A

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);
}

编译结果：

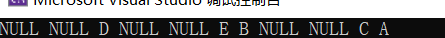
层序遍历

void LevelOrder(BTNode* root)
{
	//创建队列q
	Queue q;
	//初始化队列
	QueueInit(&q);
	//如果根结点不为空，将根节点入队列
	if (root) QueuePush(&q, root);
	//进行循环，直到队列为空
	while (!QueueEmpty(&q))
	{
		//获取队列的第一个数据，并打印
		QDataType front = QueueFront(&q);
		printf("%c ", front->data);
		//对头数据出队列
		QueuePop(&q);
		//如果左子树不为空，左子树入队列
		if (front->left != NULL)
		{
			QueuePush(&q, front->left);
		}
		//如果右子树不为空，右子树入队列
		if (front->right != NULL)
		{
			QueuePush(&q, front->right);
		}
	}
}

求二叉树的节点数

int BTSize(BTNode* root)
{
	return root == NULL ? 0 :1 + BTSize(root->left) + BTSize(root->right);
}

求二叉树叶子结点个数

int BTLeafSize(BTNode* root)
{
	if (root == 0) return 0;
	return root->left == NULL && root->right == NULL ? 1 : BTLeafSize(root->right) + BTLeafSize(root->left);
}

求二叉树的最大深度

int maxDepth(BTNode* root)
{
	if (root == NULL)
		return 0;
	return 1 + fmax(maxDepth(root ->left),maxDepth(root ->right));
}

二叉树的销毁

//二叉树的销毁
//传二级指针是为了改变指针的指向
void DistoryTree(BTNode** root)
{
	if (*root == NULL)
	{
		return;
	}
	DistoryTree(&(*root)->left);
	DistoryTree(&(*root)->right);
	free(*root);
	*root = NULL;
}

关于C语言数据结构详细解析二叉树的操作的文章就介绍至此，更多相关C语言二叉树内容请搜索编程宝库以前的文章，希望以后支持编程宝库！